算法

知识点

master 公式

T(N) = a*T($\frac{N}{b}$) + O($N^d$) 用来计算一些复杂算法的时间复杂度 如：递归

a：生成的子问题数（比如二叉树的递归遍历就是 a = 2)
b：表示每次递归是母问题的 1/b 的数据规模
N：母问题的数据规模
d：额外操作的次数
注：使用 Master 公式分析递归问题时间复杂度时，各子问题的数据规模应该是一致的，否则不能使用 Master 公式。

使用递归查找出一个数组中的最大值：

func RecursionGetMax(arr []int, l, r int) int {
	if l == r {
		return arr[l]
	}
	mid := l + (r-l)>>1
	lmax := RecursionGetMax(arr, l, mid)
	rmax := RecursionGetMax(arr, mid+1, r)
	if lmax > rmax {
		return lmax
	}
	return rmax
}

func main(){
  arr :=[]int{1,2,3,4,5}
  RecursionGetMax(arr,0,len(arr)-1)
}

上面这段代码就是用递归加二分法去将每项值返回然后再比大小，此时、母问题就是最开始掉用的函数 RecursionGetMax(arr,0,len(arr)-1) 此时数据量有 n 个，数据量是母数据的一半 所以 b = 2 。子问题是 RecursionGetMax(arr, l, mid) 和 RecursionGetMax(arr, mid+1, r) 分别查找左右两边的最大值 所以 a = 2 有两个子问题 ，每个子问题的数据量是母问题的一半所以 b = 2 。除此之外的时间复杂度为 O(1) 。 所以最后套用 master 公式：T(N) =2*T($\frac{N}{2}$)+ O(1)

满足 master 公式的算法的时间复杂度计算：

$log_ba$ > d 时间复杂度： O($N^{log_ba}$)
$log_ba$ < d 时间复杂度： O($N^{d}$)
$log_ba$ == d 时间复杂度： O($N^d * logN$)

上面的算法 a=2 ，b=2 所以满足第二条 此算法的时间复杂度为 O(N)

堆（Heap）

堆（Heap）是一种特殊的树状数据结构，通常用于实现优先队列和堆排序等算法。堆分为两种主要类型：最大堆和最小堆。

• 最大堆(Max Heap):

  在最大堆中，对于任意节点 i，父节点的值大于或等于其子节点的值。
  最大堆的根节点包含的元素是堆中的最大元素。
  

• 最小堆(Min Heap):

  在最小堆中，对于任意节点 i，父节点的值小于或等于其子节点的值。
  最小堆的根节点包含的元素是堆中的最小元素。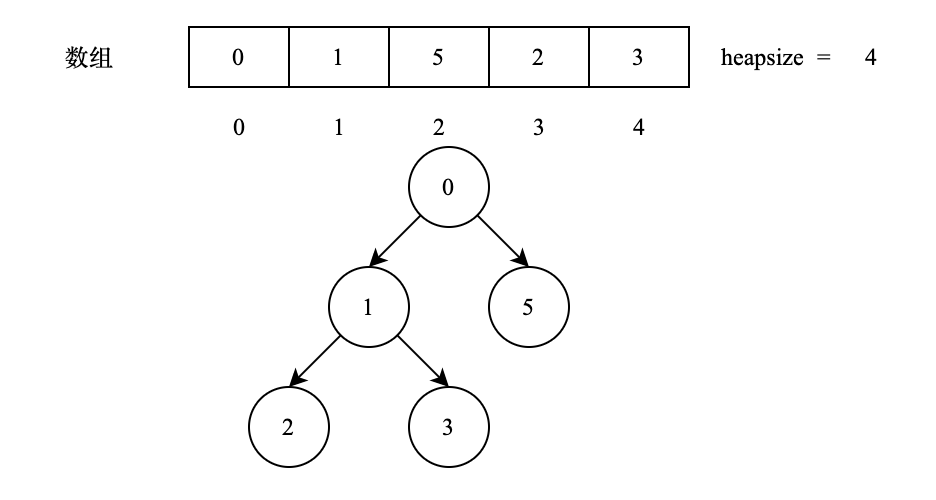
  

堆通常是一个二叉树，可以通过数组来表示。在这种表示方法中，堆中的每个节点 i 对应数组的索引 i。假设节点 i 的索引为 i，则:

左子节点索引: 2i+1
右子节点索引: 2i + 2
父节点索引: $\displaystyle\frac{i-1}2$

插入:
heapsize++ 并且将该值与父节点 $\displaystyle\frac{i-1}2$ 上的值进行比较，组成你需要的最大堆或者最小堆

删除根节点:
将最末尾的数移至根节点，heapsize– 然后从该下标出分别与左右子节点相比较，组成你需要的最大堆或者最小堆

修改:
如果是最大堆，修改后的值变大了，就与父节点比较，如果变小了就与左右子节点比较。

堆排序：

利用最大堆或最小堆根节点最大值最小值的特性，将依次把根节点删除（上面有介绍），在把堆中数据全部删除过了一遍之后就形成了一个有序的数组。要想形成生序数组就需要最大堆，反之最小堆。